For the first twenty years, since yesterday,
I scarce believed, thou couldst be gone away,
For forty more, I fed on favours past,
And forty on hopes, that thou wouldst, they might last.
Tears drowned one hundred, and sighs blew out two,
A thousand, I did neither think, nor do,
Or not divide, all being one thought of you;
Or in a thousand more, forgot that too.
Yet call not this long life; but think that I
Am, by being dead, immortal; can ghosts die?
John Donne, The Computation.
Chapter 6 contains a worked example of the heuristic methods developed in Chapter 5 for determination of which columns to partition to aid MIS range queries. Following and overview of the TSB database an example table for partitioning and a set of MIS queries are presented. Using the TSB OLTP transactions as a basis for determination of partitioning costs, the methods derived in chapter five are used to determine the numbers of partitions in each of the partitioning columns. Since the calculated WLS that can be made by single column partitioning is identical to the maximum WLS in the multi-column case, the multi-column case will be dealt with first. The maximum WLS curves derived will be used to determine the best single column to partition. Results are commented upon, assumptions and limitations discussed, and areas of further research highlighted.
All information contained in this section relates to the Trustee Savings Bank (TSB). Due to the commercially sensitive nature of the material, only the grossest generalisations are given here. All information was obtained by personal communication [THOM93].
TSB has two Transaction Processing centres. OLTP data resides at only one of these sites, and is not replicated for availability, although standby data is replicated at the other site. Relevant information for the larger site (Milton Keynes) is presented in table 6.1.
| total mainframes | 3 |
| TP database size | 15 Gigabytes |
| total accounts | 3.6 million |
| peak OLTP TPS | 100 |
| average OLTP TPS | 80 |
| average OLTP transactions per day per account | 0.65 |
| overnight batch transactions | 3 million |
Table 6.1 Real-world database statistics
The OLTP transactions used by TSB have been grouped together, and are shown in table 6.2. Also shown are the columns updated for each transaction type for the underlying database, which has, amongst others, the tables ACCOUNT and CUSTOMER containing account and customer information respectively.
| transaction type | occurrence (%) | update column |
|---|---|---|
| account enquiry | 17 | none |
| deposit | 15 | ACCOUNT.BALANCE |
| cash withdrawal | 15 | ACCOUNT.BALANCE |
| autoteller cash withdrawal | 14 | ACCOUNT.BALANCE |
| autoteller balance enquiry | 6 | none |
| other | 33 | n/a |
Table 6.2 Transaction occurrence
The only column that is updated in the transactions shown is ACCOUNT.BALANCE; approximately 50% of all transactions affect this. No information about the actual values of the increments or decrements is known, neither is any information available on the (average) data distribution of the data values.
Table 6.3 shows some of the queries contained in the "other" category of table 6.2.
| transaction type | occurrence (%) | update column |
|---|---|---|
| new account | 0.22 | n/a |
| new customer | 0.04 | n/a |
| amend name/address | 0.20 | C.TITLE, C.INITIAL, C.SURNAME, C.ADDRESS |
| credit limit update | unknown | ACCOUNT.CRED_LIM |
| where C represents CUSTOMER | ||
The transactions which are shown in table 6.3 occur with a frequency that is 2 orders of magnitude smaller than those shown in table 6.2. As has been discussed previously, the new customer and new account transactions are not relevant to the determination of partitioning columns - they are only included to clarify the general picture.
The amend name/address transaction is of interest, as it demonstrates a single transaction updating one or more attributes. (This is the reason for its inclusion, although it is not discussed further).
The example uses a single table, CUSTOMER, which is similar to the table of the same name in the TSB database. Further, the example is specifically designed to highlight the situations in which the heuristics give a definitive solution (whether positive or negative). There are three justifications for this
CUSTOMER(C_NO, INITIALS, FORENAME, SURNAME, ADDRESS, GENDER, POSTCODE, TELEPHONE, AGE, CRED_LIM, JOIN_DATE)
This table is based on the table CUSTOMER used in the evaluation of IDIOMS, but additions have been made, namely the columns GENDER, CRED_LIM, JOIN_DATE. Furthermore, there is a column for each of four address lines in the evaluation table, but only a single column is shown here. C_NO refers to a unique customer number, and is the primary key. AGE has been substituted for DOB (date of birth).
The first of the augmentations, GENDER, requires no comment.
CRED_LIM is the credit limit of the customer. In the evaluation schema this was part of the ACCOUNT table; but there does not appear to be any fundamental reason why, for exemplification purposes, it cannot be associated with CUSTOMER.
JOIN_DATE contains the date on which the "new customer" transaction was performed. In the evaluation schema this column is contained in a different table, and it contains the date on which a particular type of account was opened.
The average length of the variable length records in the TSB CUSTOMER file is approximately 256 bytes. The size of the file is thus 900 Mbyte (i.e. 3.6 million records × 0.25 Kbyte per record). Assuming that the page size of the file is 1 Kbyte, this means there are 900,000 data pages - this is the value that will be used in the following calculations.
The MIS queries used in the worked examples are based partially on the MIS queries used for the evaluation of IDIOMS, and partially from more hypothetical sources, namely [OATE91], [ONEI91], and [UNWA92].
The columns retrieved are not important, so just typical SQL WHERE clauses are shown
1. WHERE GENDER = 'FEMALE'
2. WHERE AGE BETWEEN (40 AND 50)
3. WHERE AGE BETWEEN (64 AND 66) AND GENDER = 'MALE'
4. WHERE JOIN_DATE > {current date - 6 months}
5. WHERE CRED_LIM BETWEEN (1000 AND 2000) AND
AGE BETWEEN (40 AND 50) AND GENDER = 'MALE'
6. WHERE CRED_LIM > 2500
7. WHERE CRED_LIM > 2500 AND AGE < 25
Note that the term {current date - 6 months} is not legal SQL; it should be understood that it is merely used for convenience, and would not be used in practice.
Although only seven queries are shown it should be understood that in practice a much larger set of MIS queries would be analysed over a period of many weeks or months in order to obtain a good representative sample. For simplicity this is not done; assume that the resultant QS values are representative daily values - the computation of which columns to partition, and the number of partitions for each is based on a daily average in the examples.
The reader may consider that seven MIS queries is unrealistically small as an average daily workload. This is not the case - these queries are large. As has been mentioned, some workers use the term 'data mining' to describe this type of query. Consider a typical raw disc access rate of 2 Mbyte/sec [MCKE91] for a 1 Gbyte disc. Recall the CUSTOMER file is 900 Mb, thus to scan the entire disc takes 450 seconds. This of course ignores the fact that OLTP is accessing the same disc, and only 20% of disc time is allocated to MIS [KERR91a]. Taking this into account, the observed time taken to scan the entire CUSTOMER file is 2250 seconds (i.e. 450×100/20) or nearly 40 minutes in the best case. We see that (in spite of the fact that one file scan may service more than one MIS query) seven queries is not an unduly low number.
Let us say that the data distributions are such as to result in the QS values for each column shown in table 6.4. Note that QS for JOIN_DATE is an approximation based on an assumption that growth rate is 8% a year, and ignoring compound growth, 6 months data is approximately 4%.
| query | column query size | |||
|---|---|---|---|---|
| GENDER | AGE | CRED_LIM | JOIN_DATE | |
| 1 | 0.500 | - | - | - |
| 2 | - | 0.167 | - | - |
| 3 | 0.500 | 0.050 | - | - |
| 4 | - | - | - | 0.040 |
| 5 | 0.500 | 0.167 | 0.330 | - |
| 6 | - | - | 0.167 | - |
| 7 | - | 0.117 | 0.167 | - |
| Note: Where a column is not specified in a predicate clause the QS is shown as -, rather than 1, in order to see clearly that the column is not referenced. | ||||
The four columns (GENDER, AGE, CRED_LIM, JOIN_DATE) used in the examples show the great variations in partition cost that are possible.
The partitioning costs of GENDER and JOIN_DATE are both zero for any number of partitions, since apart from corrections to input errors, the data values are not altered.
In order to avoid complex calculations which ultimately would be futile in that results would neither prove nor disprove either the validity or usefulness of the partitioning heuristics, a simplification is made in order to determine a rather gross approximation of pcostn.
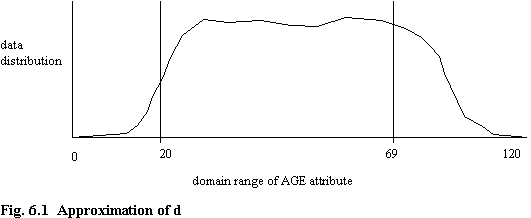
The domain of the AGE column in the evaluation tables is INTEGER. There are no CHECK clauses in the table definitions, but it is not unreasonable to assume that in practice there would be, perhaps restricting data values to the range 0 to 120. However, there would still be a high degree of data skew. A hypothetical data distribution for AGE is shown in figure 6.1. It is not unreasonable to suggest that the curve rises steeply between the ages of 16 to 20, since many people become employed around these ages. A much slower decline is expected as people die. A crude approximation is to ignore the extremes, and assume an even data distribution within the (arbitrary) range 20 to 69. Thus an approximation for d is
d = (69 - 20) + 1 = 50
Now although this value is admittedly imprecisely derived, it is sufficient to show the application of the heuristic method of determination of numbers of partitions. In the real world, of course, it would probably be wiser to perform a more detailed calculation.
Recall from chapter 5 equations (5.1), (5.2) and (5.4) for partitioning cost, pcostn, number of migrations (daily numbers are used here), and migration probability per update, migprobn, respectively.
pcostn = migration cost × number of migrations
daily number of migrations = migration probability per update × daily updates to column
migration probability per update = min(1, ((n-1)×(|UV|/|d|)))
where |UV| = absolute update value, and |d| = domain range
Since the AGE column of each record is updated once a year, the average daily number of updates to the AGE column is
average daily number of updates = (1/365) × 3,600,000 = 9863
Recall from equation 5.3 that the cost of a migration is equivalent to 40 sustained page reads. |UV| = 1, and |d| approximates to 50, thus pcostn can be written
pcostn = migration cost × migration probability per update × avg. daily number of updates
= 40 × min(1, ((n-1) × (1/50))) × 9863
= min(1, (n-1)/50) × 394520
In the evaluation tables of IDIOMS, the domain of the CRED_LIM column is defined as INTEGER. As with the AGE column, there will be data skew - possibly quite severe. Once again, a crude approximation is made. For exemplary purposes, d is made equivalent to 3000 (e.g. The bulk of data values fall say within the range 100 to 3099, and there is not a "high" degree of skew in this range). Assume that for data in this range, the average update value is 200 (i.e. £200), and the (average) update frequency to the column is once every 18 months.
pcostn = migration cost × migration probability per update × avg. daily number of updates
= 40 × min(1,((n-1) × (200/3000))) × 3,600,000/(365 × 1.5)
= min(1,(n-1) × 0.066) × 263014
Use of average update value could lead to further errors in determination of pcostn, but as will be seen later, these are unlikely to be significant with respect to overall savings.
Figure 6.2 shows the total maximum and minimum WLS for the seven queries obtained by partitioning on each of the columns (data values can be found in appendix 3). Only the three columns for which the domain is large [footnote 6] are shown, namely AGE, CRED_LIM, JOIN_DATE. The values for ST (and hence STS and WLS) were determined using the equation defining average ST for a set of queries of given size, equation (4.8), even though the queries presented here have known predicate values. The reason behind this is that firstly these queries are indeed meant to be representative, the predicate values being included for ease of understanding. Secondly, the data distributions are not known; many simplifications have been made in order to obtain an approximation for pcostn.
Table 6.5 shows the maximum and minimum WLS that can be made by partitioning the boolean GENDER column.
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | total | total × file size (K pages) | |
|---|---|---|---|---|---|---|---|---|---|
| maxWLS | -0.5 | 0 | -0.5 | 0 | -0.5 | 0 | 0 | -1.5 | -1350 |
| minWLS | -0.5 | 0 | -0.05 | 0 | -0.028 | 0 | 0 | -0.578 | -520 |
For ease of comparison, the curves for minWLS (i.e. high partitioning on other columns) and maxWLS (i.e. assuming no partitioning on other columns) for all four columns are shown on figure 6.3. Table 6.6 shows the value of n which gives greatest savings for each particular curve. Note that for the maxWLS curve for CRED_LIM, when the maximum pcost is reached, WLS once again begins to fall, and when n ≥ 18 the savings are greater than when n = 11. This effect is of no practical importance.
| column | ||||
|---|---|---|---|---|
| GENDER | AGE | CRED_LIM | JOIN_DATE | |
| maxWLS | 2 | 21 | 11 | >23 |
| minWLS | 2 | 13 | 8 | >23 |
Recall that the safe solution for determination of n for each column is to use the curve defining minWLS. This is easily done for AGE, and CRED_LIM, but a problem arises with JOIN_DATE. Since pcostn = 0 for this column, there is no point at which pcostn exceeds the scan time saving (the problem does not arise with GENDER although here pcostn = 0 also, since there can only be either one or two partitions). A sensible strategy here, as discussed in chapter 5, is to select a cut-off point where savings due to further partitioning become minimal - rather arbitrarily, say when ΔWLSn,n+1 is less than 1% of a full file scan (i.e. ΔWLSn,n+1 < 0.01 × 900 K pages). If this is done for the JOIN_DATE column, we find that the crossover point is when n=10, as shown in table 6.7, in which data values are taken from appendix 3.
| n | WLS (K pages) | ΔWLSn,n+1 (K pages) | ΔWLSn,n+1 < 9 K pages |
|---|---|---|---|
| 9 | -767 | -776 - (-767) = 9 | no |
| 10 | -776 | -784 - (-776) = 8 | yes |
| 11 | -784 | n/a |
Looking at the curves for CRED_LIM and AGE, we see that for each curve there is very little difference in WLS over a wide range of n values, so a similar approach for these columns is appropriate, as discussed in chapter 5, and the results are shown in table 6.8.
In addition to the three partitionings derived above, a further four are presented for comparative purposes in table 6.9. Alongside the partitioning details, the overall WLS over the seven queries is shown. Details of calculations are not given here, but may be found in appendix 4.
P1 is the partitioning strategy derived under the assumption that all the other columns are highly partitioned. P2 is the case where ΔWLSn,n+1 is less than 1% of a full file scan for the JOIN_DATE column only. P3 is the case where ΔWLSn,n+1 for all columns is less than 1% of a full file scan. We see that there is a difference of approximately 2.5% in WLS between P1 and P3, and the difference in WLS between P2 and P3 is approximately 0.5%.
P4, derived under the assumption that there is no partitioning on other columns, gives a WLS of -4934, which is proportionally not much less than the WLS of P1.
P5 shows that the partitioning derived under the assumption that all columns are highly partitioned (P1) is indeed, as expected, not necessarily optimal. However, the absolute increase in WLS of 500 pages (by having, for example, 15 instead of 14 AGE partitions) is a mere 0.01% of the overall WLS.
Conversely, P6 shows that using the minWLS curve to derive the partitioning does not always give sub-optimal results - by increasing the number of partitions for the CRED_LIM column from 8 (the value derived using the minWLS curve) to 9 there is a small (1700 pages) reduction in absolute WLS.
Finally, it is worth remembering that the maximum scan time saving that can be made by partitioning, ignoring any partitioning costs is -5448.5 K pages.
Clearly, there is little practical advantage in "pushing" the partitioning to its calculated limits, at least in the case of this particular example.
In the case that just a single column is to be range partitioned (which is the case with most multi-processor systems, as discussed in chapters two and three) the curves for maxWLS should be used to determine the partitioning column (see chapter 5). The AGE column is the one that gives the greatest overall WLS. The computed maximum WLS is when n = 21, but as with the multi-column case, there is little practical advantage in using this value. If a cut-off point is determined on the same basis as is used for the multi-column example (i.e. stop when ΔWLSn,n+1 < 0.01 × file size), then we find that n = 14. It should be noted that constraining the number of partitions in the single dimension case is not so important as in the multi-column case, since directory cost is linear, rather than combinatorially increasing. Further, this cost is small compared to the multi-column case. On the other hand, consideration must be given to partitioning costs with respect to OLTP costs - this has been discussed in chapter 5, but the examples contained in this chapter have not dealt with the issue, and it has been assumed that the costs shown are within allowed limits.
Since no other column are involved, the maxWLS curve for AGE directly gives the overall WLS that can be obtained by partitioning on the column.
Chapter three has shown why the number of Transaction Processor OLTP partitions and the number of MIS partitions can be determined independently. The examples above have focused purely on MIS partitioning without consideration of OLTP partitioning.
If more than one OLTP partition were needed in order to obtain the required Transaction Processing rate, the records of the CUSTOMER file would be placed on the OLTP discs associated with each Transaction Handler.
From the point of view of MIS scan time reduction, the simplest option is to partition on C_NO (customer number). A more satisfactory overall approach might be to store related customer and account records together on the same Transaction Processor disc (or set of discs). In the simple example given here, there is no easy way of doing this in general, since a single customer may have more than one account, and there is no guarantee that multiple account numbers of a single customer will be grouped together. Conversely, a single account may be jointly owned.
In practice, the possibility that a CUSTOMER record and a related ACCOUNT record are not on the same OLTP Transaction Processor is not likely to be a great problem. Firstly, it would only occur in the case that a single customer has more than one account, or that an account is jointly owned. Secondly, and perhaps more importantly, no (TSB) OLTP transactions reference both files, so no complex locking mechanisms over multiple Transaction Processors would be needed.
The foregoing is not meant as a dismissal of potential difficulties, and much further work is needed in this area.
Kerridge and North's DSDL [KERR91b] would be used to specify both the partitioning conditions, and the placement of resultant partitions to disc. As an aid to this, a DSDL illustrator has been developed [LEUN91] which enables a visual interpretation of a DSDL specification.
This chapter has shown how the number of partitions for each dimension of a multi-column partitioning strategy can be derived in practice, and comparisons have been made between different partitioning scenarios.
An observation is that for each of the partitioning columns the chosen value of n is not critical, nor is the combination of these values. In consequence, the use of maximum and minimum workload saving curves to calculate the "window of opportunity" in which the optimum value of n is known to reside is perhaps not necessary (at least in this particular case), since the values of n derived for each dimension from the minWLS curve are further reduced using the heuristic method of comparing differences in WLS with overall file size. On the other hand, the model derived in chapter five is not used to its full potential in the example, inasmuch as no potential partitioning columns are rejected - recall that rejection would occur if the maximum possible workload saving were very small, so in the general case, it would be appropriate to calculate both curves.
In this example there is just a single curve for each column's pcostn due to the fact that the underlying updates to the chosen columns affect only a single column. However, this is a detail which does not invalidate the basic model - only in the case that there is a large difference in the maximum and minimum pcostn values for each column might problems of unreliability set in. This large difference itself will only occur when a large proportion of transactions (to the relevant participating columns) update more than one column. Furthermore, in the light of the finding that scan time savings far outweigh the partitioning costs, at least for the columns chosen for the example, a relatively large difference between the maximum and minimum partitioning costs is not likely to make a large difference to the overall results.
In practice, it would be important to constrain pcostn so that it does not become unacceptably large with respect to OLTP costs. This has not been shown, an implicit assumption being that in the case of the examples pcostn is within allowed limits.
However, an interesting result is that partitioning costs are quite small compared with the scan time savings that can be made by partitioning on a given column. This is the case even for JOIN_DATE, which is only referenced once (admittedly, the query size is small). As the number of MIS queries increases (with respect to a given OLTP transaction set), the partitioning costs will become proportionally less. In the case of GENDER and JOIN_DATE, they are non-existent, and this non-existence requires a heuristic method of determining the number of partitions for the JOIN_DATE column. An interesting speculation that can be made is that perhaps incorporating partitioning costs in the model may not be necessary in the case that pcostn is very small with respect to scan time savings, and the numbers of partitions for each dimension could be determined on a similar basis to that used for JOIN_DATE. (It would still be necessary to know pcostn in order to ensure that OLTP is not unduly hindered).
Although the seven queries themselves have specific query predicates, the calculations in this chapter are all based on representative average queries (e.g. the use of the scan time equations to determine expected average scan time for a set of queries of given size). There is no guarantee that query predicates are random, and to the extent that this affects the work presented requires further investigation.
Although the results presented here indicated the viability of the method, we might consider making comparisons between this technique and other multi-column partitioning methods, in order to evaluate how advantageous the new method really is. It might be argued, for example, that although MDD [LIOU77] and Hua and Lee's adaptive data placement scheme [HUA90] (both of which are discussed in chapter 2) only use reference frequency to attributes rather than also considering query size, this might in general give results not dissimilar to those found using the new method presented in this thesis.
Consideration of one basic assumption underlying these methods shows that it is impossible to make a sensible comparison. First consider MDD [LIOU77], where the formula defining the number of partitions in a given dimension assumes that the total number of data pages needed to store the file is known. Furthermore, there is a 1:1 mapping between logical cells and physical data pages. Now although we can determine the physical number of data pages needed to store each file in the IDIOMS machine, IDIOMS does not use a 1:1 mapping between logical MIS partitions and physical data pages. It is true that each MIS partition is accessed by MIS as a single unit of access, but unlike MDD, we do not know a priori the size of logical cells. The aim of the model presented here is to determine the number of partitions in each dimension, and this does not depend upon any predetermined number of data pages in the related logical cells. Only once the partitioning has been found can we calculate the number of physical data pages for the logical cells.
A similar consideration applies to Hua and Lee's scheme [HUA90], where access frequency to attributes can be used to determine the number of partitions in each dimension. It is assumed that the ideal logical cell size is known (in terms of the number of records in that cell) in advance of calculating the number of partitions in each dimension. Once again, this is in direct contrast to the method presented in this document.
Thus, there appears to be no realistic basis for attempting a comparison between the new method and these others.
The following chapter presents overall conclusions.