"Now," said Rabbit, "This is a Search, and I've Organized it -"
"Done what to it?" said Pooh.
"Organized it. Which means - well, it's what you do to a Search, when you don't all look in the same place at once. So I want you, Pooh, to search by the Six Pine Trees first, and then work your way towards Owl's House, and look out for me there. Do you see?"
"No," said Pooh. "What -"
"Then I'll see you at Owl's House in an hour's time."
"Is Piglet organdized too?"
"We all are," said Rabbit, and off he went.
A. A. Milne, The House at Pooh Corner.
This chapter presents the main issues involved with partitioning and placement, and then focuses on issues with respect to database machines. (Chapter 3 relates these issues to the business problem and the IDIOMS architecture). Two representative multi-column partitioning methods are reviewed. Inherent limitations are discussed, leading to the conclusion that although both methods are meritorious in their own right, they are not immediate solutions to the problem of large scale concurrent OLTP/MIS access for range queries.
Before proceeding, a few definitions of the terminology used are in order. Partitioning (also known as fragmentation) is the fragmentation of a relational table into subsets, called partitions. Placement is the assignment of these partitions to physical storage media. The collective term for these is allocation. Note that some workers use the term partitioning to mean allocation.
The general aims of data partitioning and placement in database machines are to
In some cases partitioning is needed simply because a single logical relation is too large to store on a single disc.
This thesis primarily investigates the first item, with reference to the second. Incorporation of the third aspect at some later date is not precluded.
Data allocation essentially revolves around a load-balancing issue. Factors typically used in metrics include access frequency to partitions, partition cardinality, data distribution (skew), query type, and the size of relations [COPE88, GHAN90a, DEWI90b, PIRA90, PEAR91].
Much work has been done on data allocation in the field of distributed databases. Now although these are in a different class altogether from multi-processor database machines, there are logical similarities which are worth considering. Is partitioning separable from data placement? Some workers [HEVN88, SACC85] say yes, and have produced models based on this assumption. For example, Sacca and Wiederhold [SACC85] discuss database partitioning in a cluster of processors for distributed databases, with the aim of minimising the aggregate transaction costs for a given set of transactions, on a system with varying processor capabilities, and varying communication costs. Other workers say that the placement and partitioning problem is not divisible, because optimal fragmentation can only be determined with respect to the optimal allocation of fragments [CERI82].
Until recently, in multi-processor database machine research the assumption generally has been that data partitioning is subsumed within data placement strategies. Thus in Teradata's DBC/1012 [REED90], a single relation is fragmented over all the available storage nodes. The developers of both Bubba [COPE88] and Gamma [GHAN90a] suggest that data should be fragmented to varying degrees, but the limit of fragmentation is when a relation is partitioned such that a single partition is allocated to each available storage processor. Recently, the problems that arise from such simplistic methods have begun to be addressed. Ghandeharizadeh, in a further paper [GHAN90b] presents a "Hybrid-Range Partitioning Strategy" (to be commented on later), which makes a distinction between the logical partitioning of a file and the placement of partitions. This separation of partitioning and placement is a reasonable approach for the particular problem and architecture, and is also the one which has been taken with this work.
There are two basic forms of data partitioning (at least in relational terms), namely horizontal and vertical. Horizontal partitioning is generally based on predicates that define conditions on attribute values. A record is placed in a partition depending (directly or indirectly) upon the value of one or more attributes. Gamma, Bubba, the DBC/1012 and IDIOMS all use this type of partitioning. Vertical partitioning splits a relation such that some attributes appear in one partition, and others in another. One reason for this is to enable placement of frequently accessed fields on fast devices [DATE86]. Vertical partitioning is an issue that is addressed in the field of distributed database design [SACC85, HEVN88], but as far as the author is aware has not received attention in the area of multi-processor database machines. This is perhaps not surprising given that in most machines, the processors are both homogeneous and physically close; there do not appear to be any advantages of vertical partitioning over the far simpler horizontal partitioning. From now on the term partitioning refers to horizontal partitioning.
Declustering, a term introduced by the Bubba team and now widespread, is an alternative name for horizontal partitioning. It brings to mind the concept of clustering, which "is concerned with the storing in close proximity of tuples on storage devices which are referenced frequently together, thereby bringing advantages in reduced operation times on database systems" [BELL88]. Hence the term declustering is perhaps unfortunate, as it implies the opposite of clustering. Strictly this is not true. In some cases relations are "declustered" (i.e. partitioned) in such a manner as to separate records which are accessed together (e.g. round robin, value range partitioning), and in other cases the term can be used to mean range partitioning or hash partitioning, which can be considered forms of record clustering. Therefore, the term partitioning rather than declustering is used in this thesis.
The merits of clustering and declustering (i.e. partitioning) are now briefly summarised. Further details can be found later. In general, the main aim of clustering is to minimise the total work done in accessing a set of queries. Methods of clustering often attempt to place records which are frequently accessed together in the same physical storage location (e.g. disc block, disc) in order to reduce access time (e.g. fewer disc blocks accessed) and communications costs. If access frequency to data objects is known, then it is possible to place frequently accessed objects in RAM rather than on secondary storage, resulting in reduced access time.
A clustering strategy which may be acceptable on a single processor system may not be appropriate for a multi-processor system. A simple example is that clustering a file on the attribute 'GENDER' results in a reduced workload for a set of queries which reference the attribute with high frequency, and where records with only one of the two possible data value options is required. If this file is now placed on a two processor system (assume each processor has just one disc), such that records with the gender attribute value equal to 'male' are on one disc, and those with the gender attribute value equal to 'female' are on the other, the worst case scenario is that one of the discs will never be accessed (i.e. all the queries reference the same attribute value), although the total workload will still be reduced. We see that clustering in itself does not address the issue of load balancing, which is important in multi-processor systems.
The simplest method of load balancing in multi-processor systems is to partition (decluster) data such that an equal fraction resides on each storage processor. A single logical operation is physically carried out on each of these fragments of data, and assuming that the records are allocated randomly (or appear as if they are randomly allocated), then the operation time on each processor/disc will be effectively identical. Returning to our example, if the records are randomly distributed to the two discs, then the scan time on each disc will be half that of the scan time of the single processor/disc system. Now although there is a response time reduction due to parallel access, the benefits of clustering (i.e. reduced total workload) have been lost.
Using the IDIOMS architecture and the given application environment, the work in this thesis shows how it is possible to both partition (i.e. decluster) data to ensure balanced workload (for OLTP and MIS) whilst at the same time clustering data to enhance MIS performance (due to the nature of OLTP, there is no necessity for clustering).
The placement of partitions to storage media can be directly controlled by the use of a Data Storage Description Language (DSDL), rather than by file system functions. IDIOMS uses a DSDL developed by Kerridge and North [KERR91b] for this purpose. See [KERR93b] for a fuller treatment of the issues involved, and [UNWA91] for a brief discussion.
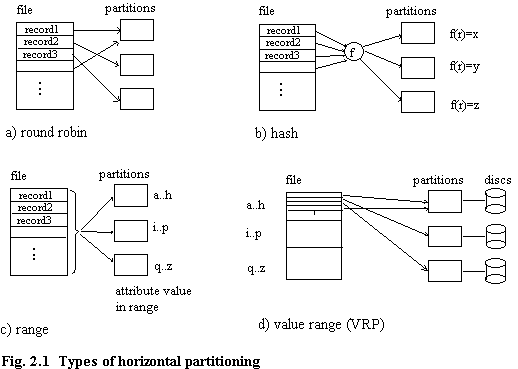
There are three basic forms of horizontal partitioning, namely round robin, range partitioning, and hash based [DEWI90b, GHAN90a, BRYA92, PEAR91]. A hybrid is value range partitioning (VRP) [HANS88]. These are shown in figure 2.1.
Round robin is the simplest form of partitioning. It guarantees balanced partition size and access frequency to partitions. Its disadvantage is that it does not aid workload reduction. To avoid ambiguity, it is worth stating that as far as this work and that of other researchers in the field of multi-processor database machines is concerned, the concept of balanced (or equal) partition cardinality (often referred to as partition size) refers to an approximate balance. For example, if one partition contains 10000 records, and another contains 10100 records they would in general be considered to be of equal cardinality.
Range partitioning reduces the search space for point queries and range queries, assuming of course, that the partitioning column and the referencing column are identical. Rather than stating this assumption each time range partitioning is discussed, the reader should bear in mind this implicit assumption. Its major disadvantage is that the access frequency to partitions may not be balanced (sometimes this can be overcome by placement methods which incorporate usage frequency) . A further problem is that unless the data distribution (i.e. distribution of data values) is considered, partitions themselves may contain widely varying numbers of tuples. However, data distribution can be measured or estimated [PIAT84], and hence equal cardinality partitions may be derived.
Hashing can reduce the search space for exact match queries and point queries, but it is generally accepted that it does not help range queries [DEWI90b, GHAN90a, HANS88]. As with range partitioning, the implicit assumption is that the partitioning attribute and the referencing attribute are identical. Ghandeharizadeh [GHAN90a] uses the term exact match to refer to retrieval of a single record (the hash is on the primary key), but if the hash is on some other field, then an exact match query would correspond to a point query (i.e. a single data value, but with possibly many records having this value).
VRP consists of (possibly only notionally) initially range partitioning a file, and then using a round robin allocation of records from each of these partitions. Hanson and Orooji claim that this guarantees parallel access, whereas (they claim) round robin does not [HANS88]. Now although it is possible to contrive a situation in which this is true, in practice for our application a round robin strategy will guarantee parallel access, as is shown later. Therefore, VRP confers no advantages to IDIOMS.
In discussions of partitioning a usual, but often implicit, assumption is that the partitioning column has a large number of different possible data values. In the case of round robin and range partitioning this is not necessary, as can be seen in the partitioning example of chapter three. However, when range partitioning is used in such cases, there is always the possibility that data skew makes it impossible to balance partition cardinality.
Readers unfamiliar with the logical model of shared-nothing multi-processor database machines are referred to chapter three for a brief review.
First methods of data placement were simplistic. In a discussion of Teradata, Schemer and Neches said, "some [points] were just basic, such as how you partition data across an array of processors. It became evident that you want a distribution of data so that a roughly equal number of the rows of each table are distributed to each processor" [SCHE84]. Now although this allows data parallelism - indeed it guarantees balanced workload since it is hash based on the primary key in the DBC/1012, it does not reduce workload for point and range queries.
If we imagine that a range partitioning strategy were used, and that equal sized partitions were placed on processors, then access frequency distribution of point and range queries may mean that some discs were accessed more frequently than others. Even in the case that range queries were evenly distributed there would be an imbalance in disc utilisation, as Ghandeharizadeh shows [GHAN90a], and which is discussed later. This is an issue that the Bubba team address [COPE88], and which the Gamma team wish they had [DEWI90b].
The aim of the study of Copeland et al. on data placement in Bubba [COPE88] is to maximise overall throughput for a given workload which consists of OLTP transactions and MIS queries (Copeland calls them all transactions, and classifies the large queries as knowledge based). Four techniques are considered in the study: declustering (i.e. partitioning), relation assignment (i.e. placement), clustering and indexing strategies, and caching. Only the first two techniques are pertinent to this thesis.
The assignment of partitions to discs is such that the access frequency to discs is approximately balanced. Partitioning has a number of constraints, the most important being that a relation will not be partitioned into more fragments than there are discs. In the application domain of Copeland's study this is a reasonable approach. He shows that full declustering (i.e. partitioning such that there is a 1:1 mapping of partitions to discs) can reduce overall throughput, mainly due to the startup costs of accessing small partitions and the communication costs for some types of transactions (e.g. those that require joins of large portions of the data). As far as the work presented here is concerned, this restriction on the degree of partitioning would be a severe limitation, because it curtails the possible workload reduction for MIS point and range queries.
A related problem is encountered by the Gamma team [GHAN90a] in their study of data allocation strategies in a multi-user environment. They consider, amongst other things, a range query with 10% selectivity. In their system there are 8 storage processors and data is sequentially stored (in conjunction with a clustered index, although this makes no material difference to the argument) , thus on each processor there is 12.5% of the total number of records of a file, and a 10% selection query will access either one or two processors. Because selection queries are randomly (but evenly) distributed, processors 1 and 8 are not accessed as frequently as the others (figure 2.2). Thus, there is a load balancing problem with this particular method of data allocation and the query type. IDIOMS does not suffer from this effect, since any range query will be directed to all discs (see discussion in chapter 3).
The Hybrid Range Partitioning Strategy (HRPS) of Ghandeharizadeh and DeWitt [GHAN90b], discussed in the following section, separates the fragmentation of a file from the placement of partitions in an attempt to overcome some of the problems described above.
HRPS [GHAN90b] works as follows (figure 2.3). A relation is sorted on the partitioning attribute. It is then fragmented such that each partition contains an approximately equal number of tuples. The number of fragments is calculated on the basis of the resource requirements of the queries and the processing capability of the system. The fragments are distributed to the processors in a round robin fashion (cf. VRP which uses a round robin allocation of tuples), and coalesced into a single file stored on that disc.
The underlying assumption regarding queries is that the selection operators use range or equality predicates, which of course is the basis of the work presented in this thesis. The aims are to
Three example queries are shown in figure 2.3. One of the small queries is localised to a single disc, whereas the other one is localised to two discs. The large query is processed over all discs. HRPS is able to deal with small relations and those with skewed data. Although it (approximately) balances workload for large queries it cannot guarantee this for a set of small queries (e.g. if a particular set of values predominates in query predicates), and as Ghandeharizadeh states, fragment assignment could be based on Copeland's work [COPE88].
So, what is the reason for not using HRPS with IDIOMS? Let's look at some further assumptions. Firstly, HRPS assumes that there is an index, and so it does not deal with selection operators that scan a file (in the cases where file scan is appropriate). The use of an index is obvious when one considers the selectivity of the queries being posed. They range between 0.001% and 10%. What Ghandeharizadeh considers a large range query, is considered small from the standpoint of the MIS queries which will be posed on IDIOMS. Furthermore, the records are ordered on disc, so the index is used only to find the boundaries of the range query. The workload reduction that does take place is due to the index and the file ordering, not the fact that the file is partitioned. What the partitioning does is to aid workload balancing.
A major limitation of HRPS is that it is one dimensional, as is acknowledged by the researchers [GHAN90b]. Indeed, this is the limitation of all the allocation strategies so far discussed. DeWitt states [DEWI90b] that the Gamma team are investigating the applicability of Grid File [NIEV84] techniques to the problem of multi-dimensional clustering. Medusa is a design by Bryan and Moore for a transputer based parallel database machine [BRYA92]; the authors state that research is being carried out on multi-dimensional allocation strategies, but no definite conclusions have been presented. The next section briefly discusses three multi-column partitioning strategies for database machines/ systems, and following this two representative multi-column partitioning strategies are reviewed; although neither was specifically designed for multi-processor environments, interesting conclusions can be drawn about multi-column partitioning techniques and the applicability to our OLTP/MIS problem.
Hanson and Orooji present results of a simulated multi-column partitioning strategy (although it is not described as such a strategy) in a multicomputer database system [HANS88]. Records for each partition are placed evenly over processing elements using either round robin or value range partitioning. Access to records is by means of B+–trees, the partitioning information is not used. Comparisons are made between round robin and VRP strategies for insertions, selections and joins. Results are presented in terms of the number of clusters (i.e. partitions) in the database, but neither the underlying data space partitioning nor (essential) details of the queries are given. It is therefore impossible to glean any useful information from this paper. One point worth noting however, is that the cost of maintenance of the (multi-column) VRP strategy becomes prohibitive as the number of attributes increases.
Ozkarahan and Ouksel present a paper entitled "Dynamic and order preserving data partitioning for database machines" [OZKA85], in which the DYOP (dynamic order preserving) partitioning strategy is presented. Could this be a solution to the problem? Let the authors speak for themselves.
"Logically, it corresponds to a dynamically maintained and order preserving direct file organization". Further, "Directory and data file partitions can be stored anywhere because their file addresses are kept in the directory". Discussing partition splitting, "This split will be made by halving the ordered range of D0 [the dimension under discussion] values hence maintaining the linear order within each resultant half" (all emphasis mine).
As can be seen, any ordering is at the logical level, not at the physical placement level. Actually, as they state, DYOP is also referred to as the Interpolation Based Grid File which was introduced by Ouksel [OZKA85]. This suffers from the same limitations as all space partitioning methods. DYOP is discussed in terms of RAP.3, a cellular architecture, and no useful parallels can be applied to the shared-nothing architecture.
Hua and Lee have proposed an adaptive data placement scheme for parallel database computer systems [HUA90] which is based on, but not restricted to, the Grid File [NIEV84]. They focus on load balancing issues, and they derive re-balancing mechanisms. From the standpoint of determination of which columns to partition, and the number of partitions for each column, their work is of no help to the issues raised in this thesis. A methodology similar to that used for the MDD structure [LIOU77] (discussed in 2.6) for determination of the number of partitions in each dimension is presented. Two points are worthy of note. First 
, where AF is the access frequency to a column and k is the number of columns (actually, they use Relative Importance Factor, which in the examples is equated to access frequency, but which need not be limited to this). This differs from Liou and Yao's MDD method, where 
. The result is that the inaccuracies shown to exist using Liou's method (appendix 1) should not arise. However, the second point to note is that since determination of the number of partitions is based on AF to columns (the same as MDD), the limitations of the MDD method remain, viz. no account is taken of the size of range queries in determination of the optimum number of partitions.
There is a paucity of information on multi-column partitioning for shared-nothing multi-processor database systems, although as has been indicated previously, there is much interest in the area. Next, two representative multi-column file partitioning methods are discussed.
Liou and Yao's multi-dimensional clustering for data base organisations [LIOU77] partitions the data space into small cells. Records in the same cell are stored on the same page of the storage device. A multi-dimensional directory (MDD) is used to find cells (pages) containing the desired records. It is an example of static partitioning in that the directory structure is not modified until some specific file reorganisation time.
The example here is a simplified version of that presented in [LIOU77]. It is assumed that a file, F, consists of fixed length records. Each domain of the keys (i.e. attributes) A1, A2, …AK consists of a set of discrete values. Consider a two dimensional case. A file is to be partitioned on attributes A1 and A2. The domain of attribute A1 is divided into m1 partitions such that each of these has the same number of records (see appendix 1 for discussion of determination of number of partitions). These partitions are called first degree cells (figure 2.4). Each of these is then divided into m2 subcells, such that each subcell contains an (approximately) equal number of records (figure 2.5). These subcells are known as the second degree cells. Each second degree cell is then assigned to a page of storage. m1 × m2 ≥ N, where N is the minimum number of pages needed to store the data. Finally, the parameters defining the partition boundaries are entered into the MDD structure (figure 2.6).
Since the partitioning is static, the overflow of buckets is dealt with by means of overflow pages which are removed at the re-organisation time.
The fact that this file structure is designed such that each cell maps onto a single data page, whereas in IDIOMS the MIS partitions consist of thousands of data pages is of no consequence. Logically, the access to partitions is identical - IDIOMS' MIS partitions are accessed (for MIS queries) in their entirety or not at all, just as the data pages in the MDD file structure are. Implementation details of the MDD directory are unimportant; the example in [LIOU77] is shown as a one-dimensional array, IDIOMS uses a DSDL [KERR91b] - at least at the top level of description - to define MIS partitioning and placement.
Liou and Yao point out that on average a query of the type "columni = value" requires N/mi (i.e. number of pages / number of partitions in a given dimension) data page accesses, and if, as is quite possible, the average number of records satisfying the condition is much smaller than N/mi, many of the pages accessed will not contain a target record. In this case the attribute could be taken out of the MDD file structure, and a single key index (SKI) could be used instead, thus resulting in a hybrid data base structure, to use their terminology. In the case of the business problem of IDIOMS, the obvious column which would not be in the MDD, but which would have an index is the primary key. Of course, this is what is done.
We see that the data space partitioning has similarities to that of IDIOMS. However, there are some differences. One is that the cells in MDD are of the same size (i.e. contain the same number of records), whereas in IDIOMS they may not be. Another is that for any partition dimension there is just one mi (i.e. number of partitions in that dimension) value. This is not an absolute requirement for IDIOMS, although it is likely in general. Two major differences are that firstly, since IDIOMS deals with orthogonal OLTP transactions and MIS queries, each MIS partition consists of thousands of OLTP data pages. The second major difference is the method that is used to derive the number of partitions for each dimension. The aim is to set the values of mi (number of partitions in dimension i) such that the average number of page accesses is minimised. This is an unrealisable ideal in the general case, and Liou and Yao suggest a heuristic solution which superficially appears reasonable (see appendix 1 for an analysis). It is predicated on the assumption that the query set only contains queries which reference a single point in any of the referenced dimensions, and thus it is not applicable to the case of range queries, as shown by the following simple example. Minimisation of the average number of partitions accessed is done by using frequency of reference to each of the attributes. Say there are 10 partitions for attributei. A (point) query of the form columni = ai requires access to N/10 pages, whatever the value of ai. In order to determine the number of pages accessed by a range query it is necessary to know the predicate values in the range query predicate, or at least the query size if we talk in terms of averages (see chapter 4). Thus simply measuring the frequency of reference to an attribute is not sufficient to determine the appropriate number of partitions in a given dimension.
The MDD file structure is static, as is that of IDIOMS; since some researchers [BRYA92, DEWI90b, HUA90] are suggesting that the Grid File may be appropriate for multi-processor database machines it is the subject of the next section. A discussion of the inherent limitations of multi-column partitioning ensues.
The Grid File was introduced by Nievergelt, Hinterberger and Sevcik in 1984 [NIEV84]. Basically, it is a dynamic mapping of data space partitions to disc buckets/pages, the mapping ensuring that buckets are reasonably well utilised (70% full or thereabouts). Each data space partition maps onto a single bucket, but a single bucket may "contain" data from many partitions. It is this dynamic mapping which differentiates the Grid File from static space partitioning organisations such as that described by Liou [LIOU77].
The operation of the Grid File is described, without loss of generality, by reference to two dimensional partitioning. Consider partitioning on attributes A1 and A2 (fig. 2.7(a)). Global intervals are imposed on each axis (cf. MDD [LIOU77], where global intervals exist only for the first level cells). Each resultant partition is known as a grid block. These are mapped to physical data pages such that each page is well occupied (approximately 70% full) (fig. 2.7(b)). A single data page may contain data from one or more grid blocks, but a single block cannot be placed on more than one page. The set of grid blocks assigned to each data page is known as a bucket region, and these regions are (hyper-) rectangular; this is called convex assignment. A fundamental principle of the Grid File is that assignment of grid blocks to buckets will always be convex.
The grid directory (figure 2.8) is a data structure which represents and supports the dynamic correspondence between blocks and buckets which is necessary due to bucket overflow and underflow. It is also used to determine which bucket(s) to access to satisfy a query. Continuing with the example, a directory consists of two one-dimensional arrays, called linear scales, and one two-dimensional array, called the grid array. The linear scales define the partitions in each of the domains, and each element of the grid array points to a single data bucket (more than one element can point to the same bucket).
A query is resolved as follows: for each attribute specified in the query the corresponding linear scale is used to convert the attribute value(s) to an index value (or values) in the grid directory. From the grid directory the address of the required bucket (or buckets) is found (figure 2.8).
If a bucket overflows (due to insertions), then some records are moved from that bucket to a new one. There are two cases, exemplified in figure 2.9. If many grid blocks are mapped to a single bucket, and if that bucket overflows, then a new bucket is used, and records that lie in one half of the space are physically moved to the new bucket (fig. 2.9(a)). The grid directory, but not the linear scales, must be updated to account for the new mapping of blocks to buckets.
In the case that a single grid block is mapped to a bucket and overflow occurs (fig. 2.9(b)), then not only must a new bucket be used, but since grid blocks are not allowed to span buckets, the grid partition itself must be split, which requires modification of one of the linear scales. Nievergelt mentions some options to determine which scale to modify, such as a cyclical schedule, or favouring some attributes by having a higher degree of resolution (e.g. if that attribute appears frequently in partially specified queries).
For the case of a shrinking file, bucket and directory cross section merging (i.e. the converse of the growing file) are necessary, but the actual options available are of no import to this discussion.
The Grid File is designed to be used with attribute domains that have many possible values; this excludes attributes such as "gender". Grid partitioning assumes that attributes are independent, whereas the strategy employed in IDIOMS does not necessarily do so.
Although the Grid File is designed to be symmetric in that no attribute is considered to be the primary access key, Nievergelt et al. do state that because query profiles in transaction processing environments vary over time, the splitting and merging policies used to deal with the variations in file content could also be used to deal with a changing query profile. For example, if a particular dimension is partitioned, but if queries no longer reference that dimension, then the directory split/merge policy could be set to a "merge only" state, so that in time when only a single partition for that dimension remains the corresponding dimension in the grid directory could be removed, or assigned to another attribute. Treatment of this issue is outside the scope of the present work, but the idea looks promising and should be investigated in conjunction with Grid File techniques in general.
The basic principles that underlie the Grid File are best explained by quoting Nievergelt.
"Two disk access principle. A fully specified query must retrieve a single record in at most two disk accesses: the first access to the correct portion of the directory, and the second to the correct data bucket.
Efficient range queries with respect to all attributes. The storage structure should preserve as much as possible the order defined on each attribute domain, so that records that are near in the domain of any attribute are likely to be in the same physical storage block" [NIEV84].
The purpose of the two disc access principle is to provide rapid response to queries accessing individual records. In order to service a query in two disc accesses the query must, according to Nievergelt et al., be fully specified. It is suggested that a request of the form, "show me this item" would trigger a fully specified query, although it is not shown how this could be done. In terms of the OLTP transactions that IDIOMS deals with this is not a reasonable approach. For example, for an office based transaction asking for information on a particular customer it may be that the customer number is known, in which case the query itself need not be fully specified in order to uniquely identify the relevant record.
The second principle is superficially a good idea, although there is a fundamental flaw in that it is based on a false premise; as has been pointed out in chapter 1, there is no point in devising a structure which is efficient in terms of infrequent or even non-existent queries, since there will always be a cost associated with the structure whether or not a query is asked. However, this is acknowledged, as discussed above in terms of the split/merge policy.
Having said this, we do want efficient range queries. Chapter 4 discusses the estimation of the average number of partitions accessed by range queries in a single dimension. Using the formula derived therein for estimating the number of partitions accessed on average by a set of queries of a given size, figure 2.10 shows how efficiency of retrieval varies with query size and the number of partitions in a given dimension, the domain of which is large. Query size is indicated on the right hand end of the curves. The reader can see that even with a large number of partitions, very small range queries are extremely inefficient. On the other hand, the largest range queries are reasonably efficient whatever the degree of partitioning.
It is claimed that the Grid File is efficient for range queries [NIEV84], although this is not quantified. Now although the statement is true, dependent on the degree of partitioning and the size of the query, it refers to the precision of the partitioning in terms of isolating the required records. (Precision is defined as number of records retrieved that meet the query specification divided by the total number of records retrieved). No mention is made of the physical organisation of the data buckets on storage media. The Grid File does not impose restrictions on physical bucket location, and as Nievergelt et al. themselves state, "Natural total orders of multidimensional data do not exist" [NIEV84]. The consequence of this is discussed in chapter 2.8, as it holds for all multi-column partition methods.
Fig. 2.10 Efficiency varies with query size and number of partitions
A rather interesting point with the Grid File on the matter of precision is that the mapping of grid blocks to buckets can destroy the efficiency of retrieval. Assume an even distribution of attribute values in two dimensions, and assume each dimension is partitioned into four. Imagine a query accesses the data shaded in figure 2.11(a). Now assume each data bucket holds data from two grid blocks. If the mapping of blocks to buckets is as shown in figure 2.11(b) then the precision is 100% (i.e. no unwanted records retrieved), however, if the mapping is as shown in figure 2.11(c), then the precision is only 50%. When many attributes are specified in an orthogonal range query, this will not be a problem, as the total number of buckets examined will be small, but if only a single attribute is specified, much unnecessary work might be done in resolving a query.
There are at least four basic reasons limiting multi-column partitioning, and they exist whether the structure is static like the MDD file structure, or adaptable like the Grid File and similar structures e.g. NIBGF [OUKS91], DYOP [OZKA85].
It is simple to show that although the precision of a query may be high this does not necessarily imply a physical efficiency of retrieval. Consider an example using the Grid File, in which an orthogonal range query has 100% precision - no unwanted records are retrieved. Figure 2.12 shows one possible mapping of grid blocks to buckets. The buckets accessed are not contiguous, and may be widely dispersed over the storage disc. If bucket size is small, this could lead to a large overhead in terms of disc arm seek time, compared with the sequential access of a single large bucket. A similar point is made in [OZKA85] regarding partition size and data bandwidth. Clearly, there is a trade-off between improving precision by reducing partition size, and non-sequential placement of partitions such that physical access time is increased.
A similar consideration applies to any static multi-column partitioning method. For example, refer back to the MDD structure. Imagine that records with data value 'B' from attribute A1 are required. In this case, four contiguous data pages (1, 2, 3, 4) will be accessed. However, say records with data value 6 (attribute A2) are retrieved - then pages 3, 6, 10, 15 are accessed; benefits of contiguous access are lost.
A second limitation is that of the directory costs. In the case of the MDD structure there is a 1:1 mapping between cells and disc buckets, thus there are 
pointers from cells to buckets. In the Grid File there are the same number of pointers from the grid blocks to the data buckets (however many or few of these there may be). Thus for a file which is partitioned in 10 dimensions, with 10 partitions in each dimension there will be 1010 pointers with either method. The storage and access of such a large directory could become a problem. Due to the adaptable nature of the Grid File, there is also the additional cost of updating the directory pointers from the grid blocks to the data buckets when a bucket splits, and the occasional modification of the linear scales.
A further problem inherent in partitioning based on attribute value (whether single or multi-dimensional) is that of migration costs between partitions. This is dependent upon not only the transaction frequencies, but also upon the number of partitions in a given dimension and the relationship between the update value and the value of the data being updated. Chapter 5 looks at this in a little more detail, for now a simple example clarifies the issue. Consider partitioning on the attributes "surname" and "account_balance". The first option ("surname") is a safe bet from the standpoint of migration frequency, since change of surname is extremely infrequent with respect to transaction frequency (either on average, or on the basis of individual records). However, partitioning on the basis of the current balance of an account might be unwise (depending on the range of the partitions), since a large proportion of transactions (in a banking environment) change this value. Indeed, this argument holds for any method that places data on the basis of the value of data, so hashing methods also suffer this limitation.
A final consideration with respect to data migration is that either a process regularly scans data and relocates appropriate tuples, or that data is moved when it is updated. The first option means that much work may be needed, even if it is found that data does not need to be moved. The latter means that although OLTP would not be affected, MIS might not give as accurate a picture as with the former option. Zorner discusses the issues of data migration in the context of DSDLs [ZORN87].
To conclude, this chapter has shown that having a large number of partitions is not practical in the context of OLTP/MIS. It is vital to restrict the number of partitioning columns in order to keep the directory to a manageable level (indeed, in [NIEV84] the suggestion is made that no more than 10 columns would be partitioned; the implementation supports a six-dimensional grid file). Semantics of the database must be known in order to prevent runaway migration costs. Physical bucket size can unduly reduce efficiency in terms of physical access, even if precision of retrieval is high. The costs of migrating data between buckets when data values change (strictly, when the new data value causes the data object to be associated with a bucket that is different from the current bucket) can be a limiting factor (see chapter 5 for a discussion and chapter 6 for a quantification).
It is worth stressing that data partition strategies and data access strategies may be mutually independent. For example, partition by hash, but access by index. In some cases they may be more closely bound, for example, the grid file as originally proposed by Nievergelt and Hinterberger [NIEV84]. Perhaps we should be thinking of a hierarchy of levels of partitioning, for example, fragmentation into partitions, further subdivision of partitions, physical storage of tuples of sub-partition on disc (clustered, random).