Then it was that men began to tie their breeches to their doublets, and not their doublets to their breeches; for it is against nature, as hath most amply been showed by Occam upon the exponibles of Master Hautechaussade.
Rabelais, Life of Gargantua.
In this chapter a cost model is derived which relates the OLTP cost penalty of partitioning on a single column to the workload reduction for MIS queries gained by such partitioning. Using the ideas developed in this model a multi-column cost model is presented, for which under a limited set of conditions it is possible to calculate an optimum value for the number of partitions for each column without reference to other columns. In the general case, to calculate an optimum value of n needs time exponentially increasing with number of columns. Since a practical rather than a purely theoretical problem is being solved heuristic solutions are presented. The abstract ideas discussed here are reified in chapter 6.
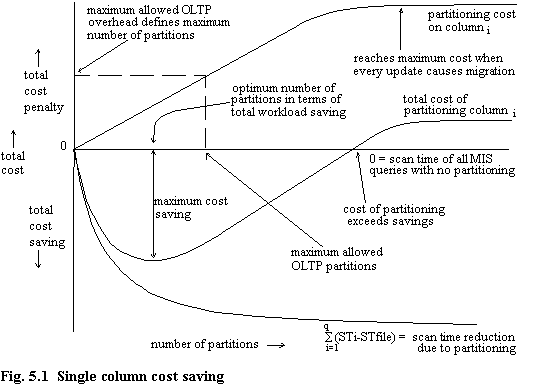
Consider for now the problem of finding the most beneficial single column to partition. The aim is to minimise the total work done. Total work consists of MIS scan time (asymptotically reducing with number of partitions) plus partition costs (linearly increasing with number of partitions), so we have to relate these as shown in figure 5.1 (discussed later). The basic OLTP costs (insertion and deletion of records, plus index update and storage requirements) can be ignored, since they are constant whatever the number of partitions. We then select the column which gives the greatest workload saving within the constraint that OLTP transactions are not unduly hindered. Thus it may be that by having a certain number of partitions the total workload could be reduced greatly, but if this means that OLTP costs are above some allowed level, then partitioning to this degree is not permitted.
There is a relationship between OLTP queries and resultant updates to any given column. The number of migrations between partitions depends on the number of updates to a given column, update value, current data value and current data placement. An average expected record migration probability per OLTP transaction can be found for any given number of partitions of a column for a given OLTP transaction set.
Since we can determine both the MIS workload reduction obtained by partitioning, and the workload increase due to partitioning, the optimum number of partitions for any column (assuming a constant proportion of OLTP to MIS queries) can be found. The column which gives the greatest total workload saving over the set of MIS queries is the one chosen for partitioning.
The multi-column cost model is based on the ideas presented above, with additional heuristics to deal with the inherent problems of the combinatorial computations involved in the precise determination of the optimum partitioning level for all of the columns.
Consideration is then given to the problem of partitioning purely on the basis of expected scan time savings for MIS, without consideration of OLTP costs.
A note on terminology is appropriate at this stage. Costs and savings vary with the number of partitions. In the general case this is an implicit assumption in the following discussion. In cases where it is necessary to make a distinction between two different numbers of partitions in a given dimension, or where considering the number of partitions clarifies the situation, this is indicated by subscripting the relevant acronyms.
Imagine we wish to partition only on the column that would lead to the greatest overall savings. Figure 5.1 shows the basic model for a single column. For each column we find the number of partitions, n, such that the cost saving is maximised, within the constraint that the maximum allowed OLTP overhead is not exceeded. Then, from all columns, select the one which results in maximum saving. Since only one column will be partitioned, the difficulties which arise in the multi-column case are not encountered.
Partition cost is shown initially increasing linearly with n, before levelling off; this is justified in section 5.2.2. Determination of the total workload reduction is discussed in section 5.2.3.
The term migration cost is used to mean the cost of a single data migration, and the term partition cost, pcostn, to mean the overall cost on a column for a given number of partitions, n. Thus
pcostn = migration cost × number of migrations (5.1)
number of migrations = migprobn × number of updates (5.2)
where migprobn is the probability, for a given number of partitions, n, that an update will cause a record to migrate. Determination of migprobn is discussed in section 5.2.2.
The total cost of a single migration between two physical partitions consists of a data page read and page write in both the current and the new partition. There is also a page read and page write of the log file and the OLTP index. Thus in total there are 8 individual page accesses. Note that for practical purposes, computation costs have been ignored, since these are tiny compared to page access costs. Index reorganisation costs need not be considered, since migration between partitions would merely change leaf nodes of the indices used in IDIOMS.
To compare like with like, these individual page accesses are expressed in terms of sustained page access (which is how MIS savings are measured). Thus the cost of a migration in terms of sustained page access is
migration cost = (sequential page access rate / random page access rate) × 8 (5.3)
Clearly, this is hardware dependent, but in IDIOMS with 1 Kbyte pages the random access rate for each disc is 100 pages/second, and the sequential rate is 500 pages/second [KERR93a]. Thus each migration is equivalent to 40 (i.e. (500/100) × 8) sequential page accesses.
Intuitively we know that as the number of partitions increases, so does the migration probability for each record. However, in some cases, for example, partitioning based on account number, there are no updates, and hence migration probability is zero for any number of partitions. Ideally, we wish to know exactly how the migration probability varies with respect to the number of partitions and the data distribution over the file.
Imagine a set of transactions for which the update values to a given column are identical. This is not always the case - there may be a range of update values - but the basic arguments presented here still hold. Let the transactions randomly access the records and increment the value of an attribute by some positive value. Assume for convenience of explanation an even data distribution and imagine an update to some record in a partition. If the value of the attribute in the record is greater than the partition upper boundary value minus the update value, the update will lead to migration (fig. 5.2). The probability of migration (i.e. the "width" of x) is equivalent to the absolute numerical value of the update value expressed as a fraction of the absolute value of the domain range.
For a single partition there cannot be migration. When n = 2, the fraction of records shaded, x, will migrate on update. When n = 3, we see that 2x records will migrate when they are updated, and so on (fig. 5.3). Rather obviously, when x is equivalent to the partition size further partitioning cannot increase migration, since at this stage all updates lead to migration. Thus migration rates for a single update value increase linearly until this point is reached, whereupon they do not increase further. (Where there are a number of different update values, the transition will not be a single point, but will vary gradually as shown previously in figure 5.1). A general formula describing migration probability, migprobn, is therefore
migprobn = min(1, (n-1) × ( |UV|/|d| )) (5.4)
Where
|d| = absolute numerical value of domain range
|UV| = absolute numerical value of update value
An interesting observation is that even if the partitions themselves do not contain equal numbers of records, as long as the data values are evenly distributed, the migration rate is not affected. This is shown in figure 5.4, where we see that with four partitions of differing cardinality, the number of migrations is the same (3x) as for the case of even cardinality partitions shown in figure 5.3.
If updates do indeed depend (unequally) on the value of one or more attributes, this basic linear relationship (before the migration costs start to level out) may not hold, even for equal cardinality partitions and with no data skew. This can be seen in figure 5.5(a), which is a rather forced example to prove the point. Imagine that there are the same number of updates as in the previous examples, but that they all affect records which have data values in the range DVi to DVi+n. In the example, since DVi+n + x is less than the upper boundary of the containing partition, no migration will occur.
One can envisage a different scenario, in which increasing the number of partitions reduces the migration probability. If there were three partitions as shown in figure 5.5(b) instead of four, most updates would cause a migration, and hence by increasing n to 4 (figure 5.5(a)), there would be a drop in migration probability. In practice these extremes are not likely to happen, but further investigation is required to quantify these abstract considerations.
Similarly, if there is data skew and even if all partitions contain the same number of records, the basic linear increase in migration probabilities of independent updates may not hold, since different fractions of the records in each partition will migrate.
However, because the data distribution is known it is possible to calculate the expected overall migration probability for any number of partitions. Although this may not be linearly increasing, it will nevertheless in general increase with n, in spite of the extreme counter example of figure 5.5. Since there are potentially a very large number of data values and update values, statistical methods of computation might be appropriate in some cases. Analysis is beyond the scope of this research. For exemplary purposes, and without loss of generality, it is assumed that migration costs increase linearly with n.
For a single query, for a given value of n, the following relationships hold:
STS = ST - file scan time (5.5)
WL = ST + pcost (5.6)
WLS = STS + pcost (5.7)
whereST = scan time, STS = scan time saving, WL = workload, WLS = workload saving, pcost = cost of partitioning.
For convenience, where the context requires, the acronyms may be subscripted, for example, STSn refers to the scan time saving that can be made when there are n partitions.
STS is always less than or equal to zero; the aim of partitioning is to determine n such that WLS has the greatest negative value.
There are two complementary ways of looking at scan time and savings; one is to consider proportional times, and the other is to look at absolute times in terms of page reads. The equations derived in chapter 4 take the former approach, which is not valid in the final analysis, since we want to relate savings to costs, which earlier are defined in terms of sustained page reads. It is worth introducing a further term at this stage, the usefulness of which will become apparent when considering the multi-column case. Let us define Access Size, AS, as the proportion of data accessed in a given dimension. For the single column case AS and proportional scan time are equivalent. The absolute ST, STS, WL and WLS are thus defined
ST = AS × file size (5.8)
STS = (AS-1) × file size (5.9)
WL = (AS × file size) + pcost (5.10)
WLS = ((AS-1) × file size) + pcost (5.11)
For a set of queries the following relationships hold
![]()
![]()
![]()
![]()
Where q = the number of MIS queries.
Note that as the number of MIS queries increases, for any given value of n, the savings in general increase, whereas the partitioning cost does not.
Now that the principles of the model have been outlined, it is time to move on to the more complex multi-column case. Note that in the following discussion, file size is normalised to 1 to avoid unnecessary computations. Of course, file size is taken into account in the computations of chapter 6.
This section shows how by considering the savings that can be made by partitioning each of the columns it is possible to determine the appropriate number of partitions for each of those putative partitioning columns.
It is shown that under the condition where transactions update a single column only, the number of migrations for each of the columns is guaranteed to be independent. In the case that more than one column is updated by a single transaction there are difficulties of analysis; a heuristic solution is proposed.
Similarly, where an MIS query predicate contains a single clause, the MIS cost benefit of partitioning is related solely to partitioning of the referenced column. However, as we know, where more than one column is referenced by a query, analysis takes exponential time. A heuristic solution is presented, and the results are then unified.
Potential migration costs for each column can be determined independently of migration costs for the other columns, under the condition that each OLTP transaction updates only a single column. Consider a transaction which updates some column, column_A. If a logical migration ensues, the record must be moved to a different partition, but this partition will be in the same dimension. There is no way an update to column_A can cause a migration between partitions of column_B (figure 5.6).
If a transaction updates more than 1 column, this in itself does not invalidate the assumptions of independence. Only if a single transaction causes migration in more than one (logical) dimension do problems of analysis arise. Consider a record with column values
column_A = 10, column_B = g.
Thus the record resides in physical partition A1B1. Imagine a certain transaction changes the values
column_A = 12, column_B = t.
Although there have been two logical migrations (from A1 to A2 and from B1 to B2) the total cost of migration is no different from the cost of moving in a single dimension, since only one record has been moved from one physical partition to another (A1B1 to A2B2).
How are we to deal with this situation? A first solution might be to assign a weighting to each logical migration, so in the example above, column_A and column_B would each be assigned a (notional) half migration. Unfortunately, this solution is not practical, since the weighting depends upon the assumption (true in the example) that both updates cause logical migration. Without knowing a priori the partitioning on all other columns than the one we are attempting to find partitioning costs for, we cannot use this approach, except for files with only a few columns.
If the majority of OLTP transactions update only a single column, then we may be justified (for practical purposes) in simply ignoring the problem. However, a more satisfactory solution is to calculate the highest and lowest possible number of migrations for each of the columns, whatever the partitioning of the other columns, in order to determine the minimum and maximum values for n (figure 5.7).
The highest possible number of migrations for a given column will be determined by the number of partitions in that column (i.e. as for single column update). The lowest number of migrations will be if the update to that column does not cause a logical migration. In the case of transactions which update a single column only, the highest and lowest number of migrations will be identical. Thus for any OLTP transaction set the maximum and minimum number of migrations can be determined for each possible value (up to some expected reasonable number) of n for each column. For a given STS curve the maximum and minimum possible WLS curves can be determined (minWLS = STS + maximum pcost; maxWLS = STS + minimum pcost).
Where MIS queries contain just a single predicate clause, the calculations for scan time and total scan time saving are exactly as for single column partitioning, since the savings on the referenced column are by definition independent of partitioning on any other column.
As is well known, a problem arises when a single query references more than one column, because now the scan time of a query depends jointly upon the partitioning of all referenced columns [e.g. LIOU77, EAST87]. Thus computation time of scan time saving for all possible partitionings grows exponentially with the number of columns.
The proportional MIS scan time saving for candidate partitioning columns can be determined for any value of n, irrespective of the partitioning of other columns. However, this saving is calculated in terms of the cost of accessing all the data in a given dimension. When no other columns are involved (i.e. single column case), then we are quite justified in equating the proportion of data accessed in the dimension to the proportion of data accessed from the file. Conversely, if scan time reduction takes place due to another column being partitioned, then the proportional scan time savings on the candidate column must be reduced by an appropriate factor in order to determine the actual scan time savings for that column.
Recall the term access size, AS, (cf. query size) is used to refer to the proportional amount of data that is accessed by partitioning on the dimension under discussion. This is independent of partitioning on any other columns. Contrariwise, scan time, ST, refers to the overall scan time with respect to the total file size, and this does depend on the partitioning of all dimensions which are referenced by a given query. Scan time is the product of the proportional amount of data accessed in each partitioning dimension.
![]()
where c = number of partitioning columns
Similarly, scan time saving due to partitioning on a given column, i, STSi, is defined as

In the single column partitioning case, or in the case that a query predicate references a single column only, or where, apart from the column under consideration, for all the other columns QS=1, ST is equivalent to AS and STS is equivalent to AS-1.
Since the scan time to solve a query in a multi-column partitioned file cannot be found without reference to the partitioning on all the columns referenced by the query a fundamental problem arises. For example, in the case of two dimensional partitioning, if we wanted to calculate the expected scan time for each possible combination of partitions in both dimensions, say up to ten partitions in each dimension, we would need 100 computations (i.e. 10 × 10). For two dimensions, this is tractable, but in the general case of many columns it is not, hence a heuristic solution is needed.
Ideally we want to do the impossible, namely calculate the scan time savings on a particular column without reference to the partitioning of any other columns. A solution to determine the scan time reduction by partitioning on a column is to use the QS of the other predicate clauses (which is independent of n), rather than (calculated) AS for each possible value of n for each column. Thus we would not need to worry about the partitioning of any columns except the one currently being dealt with. Equation (5.17) is modified to define the minimum possible scan time for a given number of partitions, minSTi, obtained by partitioning columni under the assumption that the other columns are highly partitioned.
![]()
In a similar manner, minimum scan time saving, minSTS, is defined
![]()
In general this is sensible if there is a reasonable degree of partitioning on the other columns, such that the AS in each dimension is not large compared with the corresponding QS in that dimension. This is explained by reference to figure 5.8. Let us say we want to estimate the STS on column_B that would be obtained by partitioning that column, and let us say we are examining the case of nB = 3. Further, for the sake of argument let us say there are 10 partitions on column_A. There is a query, Q1, which has QSA = 0.55 and QSB = 0.40. For convenience of discussion assume that query predicates are such that the lower boundaries of these fall on partition boundaries.
Now recall equation (5.16) defining scan time
![]()
Using equation (5.17) to determine (true) scan time saving by partitioning on column_B we obtain
STSB = (ASB-1.00) × ASA = (0.67-1.00) × 0.60 = -0.20
The equations defining minimum scan time (equation (5.18)) and minimum scan time saving (equation (5.19)) give the following results
minST = ASB × QSA = 0.67 × 0.55 = 0.37
minSTSB = (ASB -1.00) × QSA = (0.67 - 1.00) × 0.55 = -0.18
The difference between the correct scan time saving (0.-20) and the minimum scan time saving (-0.18) in this case is 0.02, that is, the estimated STSB using QSA is 2% smaller than the true STSB found using the actual proportion of data accessed (i.e. ASA). As far as determination of which columns to select for partitioning, and how many partitions to have for those columns the difference is not significant. Furthermore, this difference errs on the side of safety, as is shown later.
An objection can be raised. Consider query Q2 in figure 5.9, where QSA = 0.01 and QSB = 0.4. QSB is the same as in Q1, whereas QSA is very much smaller than in Q1. The estimate for the proportion of data accessed is 0.01 (i.e. QSA), whereas the actual proportion of data accessed on column_A in the example is 0.1.
For practical purposes, this case is irrelevant.
ST = ASA × ASB = 0.67 × 0.10 = 0.067
minST = 0.67 × 0.01 = 0.0067
STSB = (0.67 - 1.00) × 0.10 = -0.33 × 0.10 = -0.033
minSTSB = (0.67 - 10) × 0.01 = -0.33 × 0.01 = -0.0033
It is true that there is an order of magnitude difference between the true and estimated results for ST and for STSB. However, in terms of scan time saving by partitioning on column_B it matters not whether STSB is given correctly at -0.033 (i.e. 3.3% saving over total file scan time) or at -0.0033 (i.e. 0.33% saving). The absolute difference between the results is small and is not likely to affect the decision of which are the best columns to partition. Assuming column_B is chosen to be one of the partitioning columns, the error makes little difference to the determination of the optimum number of partitions as is later demonstrated.
Since a high degree of partitioning is not expected on any column, and since wasted work (i.e. AS-QS) reduces asymptotically with increasing n (see section 5.4 for a discussion of this) it is not unreasonable to assume that when the QS with respect to a column is small, the wasted work done in resolving the query is far greater than QS. Thus it would be appropriate to put a lower bound on the value of the proportion of data accessed in that dimension, and a reasonable cross-over point at which we might assume the wasted work becomes large with respect to QS would be when n is 10 (i.e. when average (proportional) wasted work = 0.1). So, we could simply use a lower limit of 0.1 for any QS value less than 0.1. Of course, this would not apply to the column for which we are attempting to find the STS obtained by partitioning.
The converse case is worth considering. If there (finally) is little or no partitioning on column_A, then the use of QSA will greatly underestimate the amount of data accessed in that dimension. For example, in the case of Q1 (figure 5.8), if column_A is not partitioned then ASA = 1.00, rather than 0.60 in the case of nA = 10, and thus
ST = ASA × ASB = 1.00 × 0.67 = 0.67
This is considerably in excess of the estimate (i.e. 0.40) previously obtained for query 1 by using QSA.
Similarly, STSB is considerably in error
STSB = (ASB -1.00) × ASA = (0.67 - 1.00) × 1.00 = -0.33
recall minSTSB = -0.18, which is only about half the true STS value. In terms of finding an appropriate value of n for column_B this will not be a problem, since the curve defining minSTS is used to determine n.
Overestimating the scan time, or conversely, underestimating the STS (by using equation (5.19)) is a safe solution. Due to the shape of the curves for partition cost and STS, this underestimate could result in a selection of n that is less than optimum in terms of maximising workload reduction. This is not catastrophic, since the absolute differences in overall WLS between the optimum value of n and some sub-optimum value are not great. This is demonstrated by means of an example. Furthermore, as is discussed later, and demonstrated in chapter 6, there is little point in attempting to achieve the greatest possible WLS.
Consider a large set of queries, with QSA = 0.5 and QSB = 0.1. The method described above to determine the maximum and minimum WLS obtained by partitioning on column_B is depicted in figure 5.10; appendix 2 gives corresponding data values. pcostn is arbitrarily chosen for exemplary purposes. The average expected AS for queries of size 0.1 in dimension B for each value of n is determined using equation (4.8).
Recall (AS-1) gives the STS on column_B under the assumption that column_A is not partitioned. (AS-1) × QSA gives the STS on column_B under the assumption that column_A is highly partitioned. Since for any n value the STS is smaller (by 50%) than for the first case, the total WLS is also smaller, since WLS = STS + pcostn.
In this particular case, the result is that the optimum value of n is different for the two cases, although it need not always be. From the viewpoint of selection of n to minimise total workload this does not make much material difference. Let us say that (finally) column_A is partitioned, but not to a high degree. The true WLS obtained by partitioning on column_B would lie somewhere between the two curves defining minimum and maximum WLS (which show large differences). However, the difference in WLS between n=3 and n=4 is small, whatever the actual WLS, so in terms of selection of n to reduce WLS no great errors are made. This is seen in chapter 6.
Now OLTP transactions have priority - they must not be slowed down unduly. Increasing n increases partitioning costs, so by underestimating the savings that could be made we
The overall solution is to determine both the largest STS (i.e. assume there is no partitioning on any other column), and the smallest STS (i.e. assume there is a high degree of partitioning on all other referenced columns). Thus for each value of n for the partitioning column under consideration we are able to guarantee a maximum and minimum STS irrespective of the partitionings on the other columns.
Now that minimum and maximum STS can be determined, it is time to unify the results to determine both which columns to partition and a value of n for each of the columns that is partitioned. For a set of MIS queries, maxSTS is simply the sum of maxSTS for each individual query. Similarly for minSTS. Determination of maximum and minimum partitioning cost has been discussed in section 5.3.1.
Figure 5.11 shows this.
Consider first the problem of which columns to partition. The true WLS that can be made by partitioning a given column will lie somewhere between the values for maximum and minimum WLS. Since the maximum WLS curve is derived under the assumption that no other columns are partitioned, it cannot in general give a reliable indication of the WLS. However, it can be used to eliminate those columns for which under any circumstances, the savings made by partitioning are minimal. At what particular point a saving is deemed 'minimal' is a matter for the DBA to decide.
Minimum WLS is derived under the assumption that there is a high degree of partitioning on other columns, and thus in general it gives pessimistic results for the estimation of WLS made by partitioning a given column. It is not safe to use minWLS to decide which columns not to partition, although it tells us definitely which columns should be partitioned.
Recall the minimum total workload saving that can be made by partitioning is when maximum partitioning cost and minimum scan time saving occur together. Similarly, the two parameters defining maximum total workload saving are minimum partition cost and maximum STS. The two resultant curves define a "window of opportunity" in which we know the optimum value of n resides. The safe solution is to use the lowest value of n thus obtained (i.e. using minimum total workload saving) - this has been discussed previously.
In some cases partitioning cost is zero, and therefore WLS will continue to increase (very slowly) as n increases, so there must be a method of dealing with this case. A reasonable approach is to stop partitioning when the WLS that can be made by further partitioning, ΔWLSn,n+1, becomes less than a small fraction of a full file scan; in the example in chapter 6 this is chosen as 1%.
Since the absolute WLS that can be made by partitioning any given column becomes very small as the optimum value of n is approached, it is reasonable to apply this heuristic to all columns, and chapter 6 shows that the resultant reduction in absolute WLS is small, whilst at the same time greatly reducing the total number of partitions.
An alternative approach to partition determination is to look at how wasted work, WW, rather than scan time saving or workload saving, varies with number of partitions. This is discussed here in terms of a single column.
WW = total work - useful work = ST - QS (5.22)
Average wasted work done in resolving a set of queries is similarly defined
avgWW = avgST - avgQS (5.23)
Figure 5.12 shows how average wasted work varies with number of partitions and query size, for an arbitrary selection of query sizes, ranging from small (QS = 0.05) to large (QS = 0.95). Scan time was determined using the 'exact' formula for expected average scan time, equation (4.8), which is derived in chapter 4. There are three salient points.
Fig. 5.12 Wasted work for varying QS and n
Observations are that
The conclusion is that purely in terms of ST reduction for MIS queries, only a moderate number of partitions is needed in any dimension, because there is little point in further reducing the small wasted work for those queries which are large. (cf. the discussion on ΔWLSn, n+1 in section 5.3.5; these two views are complementary). Similarly, for very small queries, although WW may be a significant fraction of the work, the absolute work done is small compared with a full file scan (i.e. the overall saving is large). A further consideration is that we know that for the multi-column case, partition costs are not linear, but rather are combinatorial as indicated in figure 5.13. It would be most unwise to partition highly when costs are super-linearly increasing, and benefits super-linearly decreasing with n.
In the section on single column migration costs the assumption was made that updates are independent of column values, which is true for ATM generated transactions. However, some updates are "internally generated", an example being age related motor insurance premiums. In this case the update value is a function of one or more data values in a record (see [CERI82]). There is also the possibility of statistical correlation between attribute values and update values. For example, someone with a high balance is more likely to withdraw a large sum of money than a person with a low balance (or possibly the converse holds). In practice, these considerations should not prove an insurmountable problem, inasmuch as the migration rates for any number of partitions on a column can still be determined.
The section on multi-column partitioning costs (5.3.1) suggests that the cost of more than one simultaneous logical migration is equivalent to the cost of a single physical migration. The implicit assumption underlying this is that there is just a single OLTP index. If this is not the case, then the physical cost of migration must account for page reads and writes of all indices. This does not pose analytic difficulties since only the result will differ, not the computation time of the calculation.
Once the costs and benefits of a given partitioning strategy have been determined, changes in file size itself will make little difference to the overall analysis, assuming that the query set, the ratio of MIS queries to OLTP transactions, and the data distributions do not change. Consider what would happen if the file were suddenly doubled in size. All the "internal" migrations (due to data value dependent updates, such as increment salary on age) would be doubled, since we have assumed that merely increasing the number of records does not necessarily imply changing the data distribution (of course, it may change). All "external" migrations (e.g. due to ATM usage) would be doubled, unless customer habits also changed. Total MIS savings would double (since twice as many records would be scanned), unless the MIS query set also changed.
One of the limitations of both the single column cost model and the multi-column model is that they are valid only for a fixed relationship between given sets of MIS queries and OLTP transactions. It is not safe to calculate expected savings without consideration of the semantics of the database. We also need to know about the "stability" of our calculations. For example, even if partitioning on a particular column would lead to a massive overall saving for a given MIS:OLTP ratio, it would be extremely foolish to partition if we knew that say a small proportional increase in OLTP rate with respect to MIS queries would wipe out MIS savings. Conversely, if we know that some savings will be made for a large variation in OLTP:MIS rates and for large changes in data distribution, and even if savings are not great this does not mean that it is not beneficial to partition. It just means, as stated, savings are not great - however, better some saving than none. Thus before partitioning, various "what-if" scenarios should be investigated.
As previously stated, the assumption underlying the derivation of the maxWLS curves, namely that there is no partitioning on other columns, is false except for any one column. This, however, is immaterial to the determination of the number of partitions for that dimension, not because the minWLS curve is used, but because, as has been shown, where a change in WLS between n and n+1 for any given column, ΔWLSn,n+1, is very small, the overall difference when taking the entire file partitioning into account is also small. From figure 5.10 (and results in chapter 6) it can be seen that the differences in ΔWLSn,n+1 between the maximum and minimum curves rapidly converge.
In practice, the errors that are made using the heuristic solutions presented are probably not excessive in terms of determination of appropriate partitioning columns and number of partitions for those columns. Recall that the MIS query set and possibly the OLTP transaction set are time variant, so we are not looking for an absolute optimum solution, merely a practical one.
Directory cost has not been incorporated into the model, because the cost should be small with respect to any savings. With the number of partitions in the low thousands we can be reasonably certain that this is the case, but future research should investigate directory costs in more detail.
The following chapter contains a worked example of the ideas presented here.